 Separata de la revista El Catoblepas • ISSN 1579-3974
Separata de la revista El Catoblepas • ISSN 1579-3974
publicada por Nódulo Materialista • nodulo.org
 Separata de la revista El Catoblepas • ISSN 1579-3974
Separata de la revista El Catoblepas • ISSN 1579-3974
publicada por Nódulo Materialista • nodulo.org

El Catoblepas • número 126 • agosto 2012 • página 2
§ 1
El punto de partida
de una «mapología filosófica»
1. Ante todo consideremos el término «mapa» desde una perspectiva extensional, acogiéndonos al consejo de Epicteto: Initium doctrinae sit consideratio nominis. Pero en un sentido opuesto al que ha cultivado la llamada «filosofía analítico-lingüística».
Partimos de los términos de un lenguaje de palabras (el español, en este caso; e indirectamente el francés, el italiano, el inglés, &c.) pero suponiendo que, en ellos, en cuanto significantes, nos interesan sus significados, pero no ya «mentales», en la tradición de Saussure, sino físicos. Suponemos pues que nuestra materia de investigación reside no en las palabras sino en los objetos físicos (extralingüísticos), es decir, en los mapas y en los campos representados por ellos. Y con esto no hacemos sino recorrer el camino de otros lingüistas, los que levantaron precisamente los «mapas» o «atlas lingüísticos», por el procedimiento denominado Sachen und Wörten, es decir, por la asociación de las palabras a las cosas significadas por ellas.
Si en el «atlas lingüístico» de la Andalucía de la mitad del siglo XX aparece en diversos puntos del dibujo la palabra «arado», esta palabra o significado no remite tanto a un «significado mental» sino a un dibujo esquemático del arado físico, trasunto, se supone, de los arados de la época.
2. Por nuestra parte cumpliremos este trámite ofreciendo una lista de términos o palabras conónimas del término «mapa», sin ofrecer más que algunas de las «cosas» significadas por estos conónimos. No sólo tendremos en cuenta el mapa de Tolomeo, sino también un mapa celeste, un mapamundi cosmológico, un mapa en T/O de Beato de Liébana, un mapa de España o un mapa frenológico, como el del doctor Cubí, confiando en que el lector encuentre, si lo cree conveniente, los restantes.
Presuponemos que el término «mapa», en español, tiene múltiples acepciones desplegadas a lo largo de su historia, entre las cuales median relaciones de analogía, de proporcionalidad o de atribución.
Como primer analogado podemos tomar (apoyándonos en el significado actual más vulgar del término «mapa») la acepción de mapa geográfico (estrictamente terrestre, para eliminar la «contaminación» con los mapas celestes, propia de los mapamundis terrestres), procedente, a su vez, del término latino mappa, con el significado de paño o pañuelo, pero transferido (por analogía de atribución metonímica) a ciertos contenidos gráficos en él representados. Este «primer analogado» de mapa se encuentra ya consolidado, en español, en textos de Fray Luis de León, de Fonseca o Cervantes (que pueden encontrarse en diccionarios como el de Corominas o en recopilaciones como el CORDE, de la RAE, cuya información desborda obviamente la ofrecida por otros vocabularios, incluido el de Corominas).
Lo que no es nada claro es, si el término mapa (que tomamos como primer analogado del español actual) no procedía a su vez del término mapamundi (del bajo latín, que figura en San Isidoro y en un documento de 1399). La cuestión tiene la mayor importancia desde el punto de vista filosófico, por cuanto implica el dilema fundamental siguiente: la transferencia (por atribución) de mappa-pañuelo a mapa-dibujo representativo, ¿tuvo lugar a través de dibujos representativos de la Tierra y del Cielo (por ejemplo, de una representación como la que es propia de los mapas llamados T/O, en la cual ni siquiera estaban separados los mapas terrestres de los mapas celestes, o, como también si dirá, el microcosmos del macrocosmos) a partir de la cual hubiera tenido lugar, por segregación, la de los mapas terrestres respecto de los celestes? O bien, ¿tuvo lugar a través de una «ampliación» de mapas terrestres o geográficos que hubieran precedido a los mapas celestes?
También sería preciso tener en cuenta –dejando aparte la oposición entre mapas del mundo «cósmicos» y mapas «geográficos»– la oposición entre mapas geográficos particulares o regionales –mapas de territorios rodeados de otros territorios– y mapas geográficos universales (universalidad que justificaría la denominación de «mapamundi geográfico», o, dicho de otro modo, la interpretación de la Tierra como Mundo o Globo).
En cualquier caso no olvidaremos que es a partir de las acepciones geográficas –regionales o universales– o cósmicas de los mapas como han surgido, en el español, nuevas acepciones analógicas de los mapas, entre ellas las dos siguientes (en las cuales «mapa» ni siquiera va referido inmediatamente al dibujo propio de un mapa icónico):
(1) Mapa generalista (casi siempre en femenino, la mapa), con el significado de «la flor y nata de algo». En un texto de Pérez de Hita leemos: «los caballeros le suplicaron no lo hiciese [apaciguar los bandos con quitar seis cabezas a cada linaje] porque eran la mapa de la ciudad y todos bien emparentados».
(2) Figuradamente (dice Corominas) mapa tomó el sentido de «escrito en el que se resuelve el estado de una cosa con todas sus partes».
El dilema mapamundi / mapa regional (incluyendo ahora aquí al mapamundi geográfico, con necesaria involucración a un cielo envolvente) cobra un interés filosófico de primer orden cuando nos interesamos por la idea de mapa, en la medida en la cual esta idea está involucrada con la idea de «Mundo». En efecto, mapa ¿significó originariamente mapamundi –y sólo después, por contracción, mapa regional, carta, portulano...–, o bien significó originariamente mapa regional terrestre, y sólo después, por ampliación, mapamundi?
Planteada la cuestión históricamente, y si aceptamos la tradición según la cual «el primero que hizo un mapa fue Anaximandro de Mileto» (cuyo floruit fijó el cronógrafo Apolodoro hacia el 546 antes de Cristo), el dilema toma esta forma: el mapamundi de Anaximandro, ¿era un mapa cósmico (metafísico) o sólo tenía las pretensiones de un mapamundi geográfico?
Que el mapa de Anaximandro fuera un mapa geográfico regional (por ejemplo un mapa del Mediterráneo oriental, pongamos por caso) es interpretación que puede descartarse porque, si así hubiese sido, sería imposible dar una razón por la cual la tradición se lo atribuye a Anaximandro (la situación es parecida a la que se plantea a propósito del fragmento sobre el agua atribuido a Tales de Mileto, el maestro de Anaximandro: si el agua de Tales se interpreta desde el actual concepto químico H2O, no se explica la razón por la cual Tales es considerado el primer pensador de la filosofía metafísica antigua, en lugar de ser considerado, por ejemplo, como el primer autor de la historia de la Química).
El mapa de Anaximandro será, por tanto, intencionalmente al menos, un mapamundi, de acuerdo con la condición de pensador cósmico-metafísico atribuida a Anaximandro (que fue también precisamente quien acuñó el término «cosmos»). Pero, ¿del mundo terrestre –que Anaximandro consideraba como un disco cilíndrico flotando en medio de los astros (que tenían que ser representados forzosamente en el mapa)– o del mundo celeste? Con esta última pregunta pretendemos suscitar la duda sobre la posibilidad misma de una separación clara y distinta entre los mapamundi terrestres y los mapamundi cósmicos (por ejemplo: un mapa T/O, ¿es terrestre por la T, cuando se suprimen las alusiones «teológico trinitarias», o es celeste por la O que rodea a la T?). Y, por tanto, la duda sobre el alcance mismo de un mapamundi. En el caso del mapa de Anaximandro: ¿cómo podría atribuírsele este mapa sin presuponer que en él debiera estar de algún modo representado el cosmos y el apeiron, siendo así que ni el cosmos, ni menos aún el apeiron (términos ambos acuñados por Anaximandro), son siquiera representables?
3. La lista de términos conónimos de mapa que, sin pretensiones de exhaustividad, tenemos presente en este momento, es la siguiente (remitimos a nuestro rasguño sobre los «Conónimos», El Catoblepas, 67:2, septiembre 2007), advirtiendo que los términos de la enumeración son, muchas veces, antes clasificaciones de conónimos (es decir, conjuntos de conónimos) que términos conónimos, como ocurre cuando hablamos de «mapas celestes convexos»:
1. Mapas geográficos terrestres.

Sebastian Münster, Cosmographia, 1544, Hispania
2. Mapas geológicos en esbozo («croquis»).

«Croquis geológico del conjunto de los Pirineos, según R. Mirouse en Les Pyrenées, de la montagne á l'homme, 1974.»
3. Mapas terrestres degenerados, fantásticos o imaginarios (mapas que no son mapas, sino grafos de mapa).

Utopiae insulae figura (Tomás Moro, De optimo reipublicae statu, deque nova insula Utopia, Lovaina 1516).

Mapa ficción geográfico-político de Euskal Herria.
4. Planos de ciudades o de instalaciones suyas.

Plano de las líneas del Metro de Madrid en 1928.
5. Mapas geográficos especializados (como por ejemplo un mapa de ferrocarriles o un mapa de ríos).

Mapa de carreteras de España y Portugal.
6. Cartas de marear (con las series de longitud y latitud en las franjas, &c.).

Carta de marear de la Isla de Cuba
7. Cartas portulanas de navegación, sobre pergaminos de ovejas.

Mapa portulano atlántico de Juan de la Cosa (1500).
8. Mapas portulanos circulares, sobre pergaminos de ternera.

Mapa portulano circular (1450).
9. Cartas marinas de navegación, cartas hidrológicas (no bien distinguidas de las cartas de navegación del epígrafe 6).

Carta marina de la Bahía de Ceuta.
10. Mapas de fondos marinos, mapas sin oceános.

Worl Ocean Floor, según Bruce Heezen y Marie Tharp, dibujo de H.C. Berann, 1977
11. Mapas políticos, religiosos, &c.

Mapa de religiones del mundo (desde la perspectiva de las llamadas, desde Max Müller, «religiones del libro») con la Biblia común a católicos y protestantes.
12. Mapas de cultivos (coordinables, muchas veces, con los mapas religiosos).

Mapa mundial de cultivos genéticamente modificados 2008.
13. Mapas celestes desde una perspectiva cóncava (los mapas representan a la esfera celeste desde abajo del cénit celeste, y desde dentro de ella).

Mapa celeste cóncavo (recreación de un grabado clásico por Flammarion). El explorador (o sujeto operatorio) se sitúa en una perspectiva cóncava, y asimismo se supone que, dentro de la «cueva», va avanzando hacia el horizonte límite de esta concavidad apotética –que algunos cosmólogos actuales cifran a una distancia de 10.000 millones de años luz–. Al llegar al horizonte saca la mano para «palpar» el mundo exterior en perspectiva convexa.
14. Mapas celestes desde una perspectiva convexa (es decir, considerando a las esferas celestes como percibidas por algún sujeto que las contempla desde la convexidad de su superficie).

Mapa celeste convexo.
15. Mapas terrestres-celestes.

Mapa T/O en la primera edición impresa de las Etimologías de San Isidoro de Sevilla (Augsburgo 1472). Ante este género de mapas alcanza un gran interés la lectura de textos como el siguiente, del fraile jerónimo Héctor Pinto, Imagen de la vida cristiana (1571): «Dice Platón que entonces serán las ciudades bienaventuradas cuando los filósofos rigieren o cuando los reyes filosofaren. Por esa autoridad, dijo el matemático, se prueba que es necesaria a los príncipes y a todos los gobernadores la filosofía, en especial la matemática, para saber el sitio del mundo y el movimiento de los cielos y las navegaciones y climas y constelaciones y para saber situar una ciudad y ordenar un ejército y guiar una armada y otras cosas de esta calidad que pertenecen a un perfecto príncipe. Esto movió a Ptolomeo, rey de Egipto, a darse tanto a la matemática que venció en ella los filósofos de su tiempo y escureció la memoria de los antiguos. Dios hizo el mundo y Ptolomeo lo describió y matizó. A este famoso rey imitó el rey Don Alonso de Castilla en la composición de sus tablas matemáticas. Julio César, aquel ilustre emperador y espantoso capitán, se dio tanto al conocimiento del curso del sol, luna y estrellas, y filosofó tan altamente en las cosas de la matemática, que tuvo tanta guerra consigo mesmo sobre la ciencia cuanta tuviera con sus enemigos sobre el imperio. Y estimaba tanto las letras que aprendiera como las tierras que conquistara. Y no conquistara él tantas, si no las viera dibujadas en el mapa mundi que inventó Anaximandro, como lo cuenta Eratóstenes y refiérelo Estrabón en el su primero libro de la geografía. [...] ¿Cómo se pudiera navegar sin matemática? ¿Cómo se pudieran atravesar las dudosas olas de las inmensas aguas y hacer carrera real y derechísima por ellas sin conocimiento del norte y de las estrellas y de los círculos celestes? La aguja y carta de marear, ¿qué cosa es sino matemática? Esas regiones tan separadas y tan extrañas, ¿cómo fuera posible descubrirse y conquistarse, si los nuestros no fueran instruídos en el conocimiento de los movimientos del cielo, en los grados de la altura, en los círculos y cursos de los planetas, en la división de los climas, en la mapa, en el astrolabio, en el cuadrante, en la propriedad y variedad de los vientos, en los eclipsis, en la arte de la navegación, en la cosmografía y sitio del mundo, en la cantidad de la tierra, en la naturaleza de los elementos y finalmente en el conocimiento de la esfera, lo cual todo consiste en la matemática?»
16. Mapas galácticos (por ejemplo, el AINUR: Atlas of Images of Nuclear Rings, presentado en 2009 por el Instituto Astrofísico de Canarias).

Anillo nuclear NGC1512 del AINUR (del Instituto de Astrofísica de Canarias)
17. Atlas (un mapa o una colección de mapas celestes y terrestres en los que la Tierra está tomada globalmente y como sostenida en los hombros del hijo de Japeto, que pisa sobre nubes). Mercator jugó ambiguamente con el rey Atlas de Libia y con el titán Atlas.

Mercator, Atlas minor (portada de la edición de Amsterdam de 1634).
18. Planisferios, cartas en las cuales la esfera terrestre o celeste se representa en un plano.

Mercator, Orbis Terrae compendiosa descriptio (1587).
19. Mapas esféricos (como la Sphera del Mundo) versión de Jerónimo de Chaves del Tratado de Sacrobosco, Sevilla 1545).

Sphera del Mundo (según la versión de Jerónimo de Chaves del Tratado de la esfera de Juan de Sacrobosco, Sevilla 1545)
20. Esferas armilares.

Esfera armilar (≈ 1582), Biblioteca del Monasterio de El Escorial
21. Planetarios.
22. Mapamundis cosmológicos (por ejemplo, representaciones cinematográficas en Omnimax del cosmos en evolución, desde el Big bang hasta las ciudades industriales de nuestro siglo).

La Galaxia del Sombrero, según IMAX (dicha también M104 o NGC 4594, descubierta por el francés Pedro Mechain, que se murió en 1804 de fiebres en Castellón de la Plana, mientras medía el meridiano).
23. Atlas anatómicos.

Los famosos dibujos «arquitectónicos» de Vesalio en el siglo XVI, o los de Crisóstomo Martínez en el siglo XVII, serán reinterpretados como «Atlas anatómicos» más tarde, de hecho, a partir del siglo XIX. La transferencia del término atlas, incorporado a los mapamundi cósmicos, a los dibujos anatómicos, estaba virtualmente contenida en la doctrina del macrocosmos (universo cósmico) y del microcosmos (el hombre). Existen mezclas pintorescas de mapamundi y mapas «anatómicos» (antropomórficos):
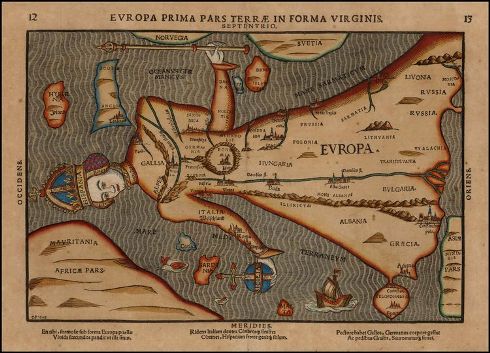
Europa prima pars terrae in forma virginis (en la versión de Heinrich Bünting, 1581).
24. Mapas frenológicos.



Gall y Cubí popularizaron en el siglo XIX los mapas frenológicos. Bretón de los Herreros, en 1845, saludaba así a la nueva disciplina frente a quienes se reían de ella: «Luisa. ¡Supersticiones ridículas! Ceferina. Brujerías... D. Manuel. No por cierto. La frenología es ya digna de entrar en el gremio de las ciencias, pues se apoya en muchos experimentos notables, y la defienden autores de mucho mérito.»
25. Mapas anatómico neuronales.

Los más divulgados fueron los «Homúnculos» elaborados por J. F. Fulton, basándose en las exposiciones de W. G. Penfield y E. Boldrey, «Somatic motor and sensory representation in the cerebral cortex of man as studied by electrical stimulation», revista Brain, 1937, 60(4):389-443. Los homúnculos pretenden ser «demostrativos» de la posición y extensión relativa de la representación de las diversas partes del cuerpo en el área motora o sensorial del cerebro.

Otros mapas neuronales suponen que la información retiniana se cartografía en el NLG –núcleo lateral geniculado– del tálamo): «Fig. 45. Mapa esquemático del córtex visual izquierdo (sin desplegar) de un mono lechuza. Sólo se ven la V1 y la V2. El dibujo de la izquierda muestra el campo visual derecho. Nótese los símbolos utilizados para indicar las distintas partes, símbolos que se repiten en el mapa de la derecha», Francisc Crick, The Astonishing Hypothesis, págs. 173 de la edición española, Debate, Madrid 1994.
26. Mapas metafísicos ontoteológicos, por ejemplo, varios de los que ofrece Roberto Flud, en Utriusque cosmi. En este epígrafe incluiríamos también cuadros-mapa como el Entierro del Conde Orgaz o Cristo en brazos del Padre Eterno de El Greco, en los cuales los vectores arriba, abajo, derecha, izquierda, delante, atrás, juegan un papel decisivo.

El Greco, Cristo en brazos del Padre eterno [La Trinidad] (1577-1580, Museo del Prado, Madrid.) Este cuadro de El Greco puede interpretarse, sin violencia, como un mapa cósmico, puesto que sus figuras están organizadas siguiendo vectores norte/sur, derecha/izquierda y delante/detrás; un mapa intencionalmente tridimensional, concebido «desde las alturas», desde la Santísima Trinidad: Espíritu Santo, Padre e Hijo, para seguir la línea descendente del cuadro; pero con alusiones pictóricas a los coros celestiales (querubines, arcángeles, &c., como antropomorfos alados), los ángeles (cabezas aladas sobre las cuales se «adelanta» la pierna izquierda del Hijo) y a unas nubes atmosféricas tras las cuales se encuentran sin duda los planetas y la Tierra.

El Greco, El entierro del Conde de Orgaz (1587, Iglesia de Santo Tomé, Toledo.) La organización del mapa cósmico involucrado en este cuadro es similar a la que hemos atribuido al cuadro precedente, si bien la perspectiva está ahora concebida por oposición a la primera, desde la Tierra, en la que se desploma el Conde de Orgaz.

«Aut in forma Trianguli, quoniam, ut in corpore Triangulari tres reperiuntur anguli distincti in unico subjecto, sic in unica Deitate existunt tres personae distinctae nullatenus ab unitate divisae. Atque, ut nobis videtur, non inepte potest incomprehensibilis illa & infinita Trigoni divini extensio secundum humani captus possibilitatem describi demonstratione sequenti. Demonstratio.» (Roberto Flud, Utriusque cosmi maioris scilicet et minoris Metaphysica, physica atque technica Historia, Oppenheim 1617, página 20.)
27. Mapas cosmogónico metafísicos.

«Ut in mundi primordio, ubi tenebrae cujusque coeli cum partibus lucidis, quas viscositas spirituum in illis conclusorum, informationis que avidorum amplexa est, luctabantur in unica eademque massa, in regionem elementarem contracta.» (Roberto Flud, Utriusque cosmi..., Oppenheim 1617, página 41.)
28. El hombre microcosmos (prefiguración del Ego trascendental) como mapa del macrocosmos.

El Hombre de Vitrubio según Leonardo. Como comentario de este hombre-mapa cabría recordar el texto siguiente de Fray Luis de Granada (Introducción del símbolo de la fe, 1583): «Por lo cual lo llama San Gregorio "toda criatura", por hallarse en él la naturaleza y propiedades de todas las criaturas. Y por eso lo crió Dios en el sexto día, después de ellas criadas, queriendo hacer en él un sumario de todo lo que había fabricado, como hacen los que dan o toman cuentos por escrito, que al remate dellas resumen en un renglón la suma de todas ellas, de modo que aquel sólo renglón comprende todo lo que en muchas hojas está explicado. Y lo mismo en su manera parece haber hecho el Criador en la formación del hombre, en el cual recapituló y sumó todo lo que había criado. De aquí es que con mayor facilidad conocemos por aquí las perfecciones divinas, que si extendiésemos los ojos por todo el mundo, que es cosa que pide muy largo plazo. Y por esta causa los cosmógrafos hacen una mapa, en que pintan todas las principales partes y naciones del mundo, para que con una breve vista se vea dibujado lo que en su propria naturaleza no se pudiera ver en muchos años. Pues así podemos decir que el hombre es como una breve mapa que aquel soberano artífice trazó, donde no por figuras, sino por la misma verdad nos representó cuanto había en le mundo. Y cuanto esta mapa es más pequeña y familiar y más conocida de nosotros, pues anda en nuestra compañía, tanto nos da más claro conocimiento del Criador.»
29. Mapas ontológicos icónicos.

Mapa del espacio antropológico (en «Sobre el concepto de espacio antropológico», El Basilisco, nº 5, 1978, página 58). Conviene confrontar este mapa icónico con los mapas geométricos del espacio antropológico reproducidos al final de este rasguño.
30. Mapas anicónicos (secuencias de palabras o de letras que pretenden esquematizar conspectivamente los contenidos de un campo en cuanto distinto de otros). El mejor ejemplo histórico serían los conjuntos formados por las llamadas palabras clave, extraídas eventualmente de un thesaurus de referencia, que suelen ser exigidas por los editores de publicaciones científicas o paracientíficas. Estos conjuntos de palabras claves, descriptores, &c., satisfacen plenamente la definición de las acepciones analógicas de mapa que hemos reseñado en § I, 2 de este rasguño, a saber, la acepción (1) documentada por el texto de Pérez de Hita («los [caballeros seleccionados] eran la mapa de la ciudad y todos bien emparentados»), y la acepción (2) de mapa indicada por Corominas: «Escrito en que se resuelve el estado de alguna cosa con todas sus partes» (Diccionario crítico etimológico castellano e hispánico, 1980, III:836).

Citas a Mendel antes de su redescubrimiento (según Eugene Garfield, «Citation Indexing for Studying Science», Nature, 227:669-671, 1970.)

Los PSI (Permuterm Subject Index), diseñados por Eugene Garfield en 1964, fueron introducidos desde 1966 como una sección más del SCI, Science Citation Index.

Tabla de relaciones del término «Desarrollo económico y social» a partir del Thesaurus de la Unesco (según Francesca Severino, 2005.)
* * *
Objetivo secundario de esta enumeración de conónimos es el de desbloquear la «fijación» del significado de «mapa» a su acepción de mapa geográfico (que algunos geógrafos reivindican, gremialmente, como instrumento característico de su disciplina).
§ 2
El término «mapa»
desde una perspectiva intensional
1. Partiendo de una enumeración de las cosas denominadas «mapas», de un modo generalmente reconocido en una tradición bien consolidada, planteamos la cuestión acerca de si todas estas «cosas» que llamamos «mapas» participan o no unívocamente de una definición. Por ejemplo, los elementos de una clase distributiva participan de su definición, pongamos por caso, como ocurre con los elementos de la clase «figuras triangulares», que participan distributivamente de la definición euclidiana del triángulo como «polígono de tres rectas que se cortan dos a dos formando tres ángulos cuya suma equivale a dos rectos». Esta definición tiene como modulación analógica elementos tales como «triángulo birrectángulo» (un triángulo dos de cuyos ángulos suman ya dos rectos, de suerte que no puede hablarse de un «corte de rectas dos a dos», puesto que dos de los lados se cortan en el punto de infinito, es decir, no se cortan).
La cuestión planteada arranca de la sospecha de que la mayor parte de las «cosas» denominadas «mapas» participan distributivamente de una definición unívoca común, pero que, sin embargo, hay otras muchas cosas «denominadas mapas» (en principio, con igual derecho) que no satisfacen la definición unívoca, sin que por ello carezcan de toda conexión con los mapas que constituyen la «región unívoca» de la «extensión».
Hay mapas de gran importancia que no satisfacen la definición unívoca, sin por ello merecer el nombre de mapas disparatados o equívocos. Se supone que existe algún «puente» capaz de establecer la conexión entre los mapas, en sentido unívoco, y los mapas en sentido analógico.
En conclusión, mapa no sería un concepto unívoco, salvo para un subconjunto o región de su extensión; pero habrá, sin embargo, mapas en sentido analógico, aunque internamente vinculados a la definición unívoca, a la que modulan por motivos diversos, como pueda ser el desarrollo límite de algunos de sus componentes (como es el caso de las rectas-lados del triángulo birrectángulo antes considerado), participando de algún modo de la definición.
Los mapas, en su conjunto, constituyen así una «constelación de conónimos» que, considerada globalmente, nos obliga a mantener que el significado de mapa es antes que un concepto unívoco (que se manifiesta en contextos sobre todo tecnológicos), una idea analógica, común a los mapas estrictos (en sentido unívoco) y a los mapas analógicos. Un concepto que nos aproxima a una idea más afín a aquellas ideas filosóficas, oscuras y confusas, pero no por ello meramente subjetivas, sino acaso lisológico-objetivas (como pueda serlo la idea de «Ser», la idea de «Sujeto», pero también la idea de «Materia M», &c.).
No cabe confundir las relaciones de correspondencia biunívoca entre el dibujo o grafo de un mapa y su campo (que pueden mantener relaciones de uno a uno, es decir, uniunívocas) con las conexiones de uno a varios (uniplurívocas) del grafo con campos diversos (como si hubiese transitividad en la conexión). La correspondencia biunívoca del sello o cuño –de puntos o rasgos diatéticos pertinentes– con la moneda, en el proceso diatético de la sigilación, no quiere decir que el cuño tenga una relación uno a uno con la copela (como si un cuño sólo pudiese proyectarse causalmente con una única copela, a la manera de los vaciados escultóricos con una única copia); las conexiones del cuño o molde con las copelas son uniplurívocas, sin perjuicio de la correspondencia biunívoca del cuño con cada copela. Cada moneda acuñada, sin embargo, no es un cuño para las otras monedas de la serie.
El carácter uniplurívoco de la relación entre el grafo o dibujo del mapa y su campo, permite reconocer la posibilidad de que el mismo dibujo del mapa pueda a la vez representar a campos totalmente diferentes, como pudiera ser el caso de los mapas de Roberto Flud en su obra Utriusque cosmi [macrocosmos y microcosmos] de 1617, en los que aparece un dibujo susceptible de ser interpretado tanto como un mapa cósmico (en el que los cuatro elementos aparecen representados en un mundo cuyo cielo está rodeado por una cadena de nubes acuosas) o como un mapa anatómico (un vientre con los intestinos u otros órganos, que también se suponen constituidos por los cuatro elementos).
2. Como definición de la parte unívoca del término mapa, utilizaremos la siguiente:
Un mapa es un objeto físico o corpóreo, que denominamos grafo o dibujo del mapa (grabado en un paño, en un pergamino, en una tabla...), equiparable al dominio de una relación aliorelativa y no reflexiva (puesto que rechazamos la posibilidad de un «mapa de sí mismo»). El mapa, como objeto físico, puede estar constituido por un sólido corpóreo E3 (por ejemplo, una esfera armilar) o por partes formales suyas, de dimensión E2 (superficies esféricas, cilíndricas o planas) y aún E1 (una línea geométrica, recta o curva, que desempeña muchas veces el papel de mapa de un río, de una carretera o de una línea ferroviaria).
Ahora bien, el dibujo o grafo del mapa, correspondiente al dominio de una relación, es sólo un componente genérico del concepto del mapa que, por sí mismo, no podría ser considerado como tal, si nos atuviésemos a los términos de su propio grafo o dibujo, es decir, si el grafo o dibujo se equipara a un significante de Saussure, considerado en su suposición material. El dibujo o grafo del mapa, como ocurre con las palabras del lenguaje de palabras, sólo asume la significación de mapa en suposición formal. Es decir, una suposición que desempeña una función alotética mediante la cual manifiesta su correspondencia con otros conjuntos finitos de objetos físicos con los cuales mantiene correspondencias biunívocas de representación isomorfa. A estos conjuntos de objetos los consideramos como el codominio de la relación aliorelativa.
El grafo del mapa se vincula originariamente a su codominio alotético, no tanto por una relación (que es posterior), sino por una operación (vinculada al «demiurgo» del mapa). Un demiurgo (o sujeto operatorio) que utiliza el grafo (grabado en un soporte) como guía para analizar el campo, y que utiliza el campo seleccionado por el significado para corroborar la propia estructura del significante. Este viene a equivaler, por tanto, a una imagen o icono del significado, si bien el icono se adapta al campo. La adaptación es recíproca, pero intransitiva (el modo de la transitividad no es obligado, y por ello tampoco la reflexividad). Las operaciones por las cuales el sujeto utiliza el grafo para actuar sobre el campo, y las recíprocas, son fundamentalmente autologismos, si bien internamente engranados con dialogismos (en la medida en que el demiurgo del mapa, o bien es un demiurgo colectivo, o simplemente es un demiurgo individual que puede ser sustituido por otros).
En conclusión, los puntos del grafo del mapa constituyen una selección (entre los infinitos puntos del soporte, o dominio, y los puntos del campo, o codominio) que sólo puede haber sido establecida por un sujeto operatorio, el que denominamos demiurgo, recordando que el «Ego trascendental» puede asumir las funciones del demiurgo de un Mapamundi: remitimos a nuestro artículo «El puesto del Ego trascendental en el materialismo filosófico» (El Basilisco, número 40, 2009). Demiurgo que ha seleccionado en el codominio los puntos (accidentes, relaciones, &c.) pertinentes o significativos, puesto que el mapa no es una estructura a priori que se arroja al campo como una red destinada a seleccionar aleatoriamente contenidos suyos. El mapa es una morfología que, en relación con su campo, mantiene un isomorfismo pragmático cuyo fundamento no reside en el grafo, ni en su campo, sino en la involucración entre ambos. Si los mapas que utilizó Colón o Juan de la Cosa sirvieron de guías a sus respectivas navegaciones, y estas consiguieron transformar la hipótesis de la esfericidad de la Tierra (establecida por Eratóstenes, Posidonio, Tolomeo) en una tesis científica verdadera, fue debido no a un «ajuste» geométrico entre los diversos mapas del globo, sino al ajuste de las partes de la Tierra descubiertas con otras partes del propio globo terráqueo (un ajuste que sólo pudo ser establecido tras múltiples aciertos y rectificaciones parciales).
3. Consideraremos aquí al mapa como institución, es decir, como una estructura supraindividual, debido a que, aunque sea levantada por un individuo para fines personales (el caso del croquis que asegura a alguien el recuerdo del sendero por el que puede recuperar el arma o el tesoro escondido), sin embargo puede ser utilizado por otros individuos humanos que cumplen determinadas condiciones.
El mapa es una institución de la clase de las que hemos llamado instituciones pragmáticas (remitimos a nuestro «Ensayo de una teoría antropológica de las instituciones», El Basilisco, nº 37: 7. Instituciones pragmáticas [este epígrafe falta, por error, en el original citado]).
En efecto, el mapa quedaría desvirtuado como tal si se cortasen las conexiones pragmáticas entre el sujeto operatorio que utiliza los grafos y el campo de su aplicación. Un mapa no pertenece propiamente a la clase de las instituciones semánticas, aunque es reducible, por abstracción, a la condición de una representación intencional-especulativa de un dominio de referencia; menos aún pertenece a las clases de las instituciones sintácticas. El mapa es institución pragmática que participa tanto de las figuras autológicas como de las dialógicas (por la sustituibilidad de unos sujetos por otros), e incluso, desde luego, de las figuras normativas. Una carta de navegación sólo funciona como tal cuando actúa como norma-guía de las operaciones del piloto al tomar un rumbo en lugar de otro, o incluso cuando actúa como norma negativa en el momento de rectificar un rumbo señalado por el mapa.
Los mapas están intercalados en diversas y heterogéneas instituciones humanas, comenzando por las señalizaciones del propio terreno (ya en los pueblos más primitivos). Una red de señales que podrá retrospectivamente considerarse como un «protomapa».
Incluso cabría hablar, en Etología, de «protomapas» (o de señales «mapiformes») aludiendo a las redes de señales sobreañadidas al territorio del bosque o a sus doseles por hormigas, aves o chimpancés, cuando intentan orientarse en sus viajes, a veces, de cientos de kilómetros. La misma «danza redonda» de las abejas, descubierta y descrita por Von Frisch, ofrece aspectos de un protomapa ejercitado por dichos insectos.
4. Como institución, el mapa, cualquiera que sea, asumiría las características generales que consideramos propias de toda institución (artículo citado, págs. 21-29).
(1) Ante todo la característica de «estructura hilemórfica». Un mapa tiene una materia (necesariamente externa a los grafos), porque el mapa no es reflexivo (como pretendió serlo el llamado mapa de Royce), que podemos identificarla con su campo de aplicación (el mapa no se dibuja «en abstracto», es decir, con abstracción de toda materia definida, sino que supone necesariamente un campo al que, desde luego, irán dirigidos los grafos del mapa). El mapa tiene además una forma, que comprende al conjunto de sus grafos, establecido por el sujeto operatorio.
(2) Como segunda característica señalaremos su condición de institución compleja, resultante del encadenamiento de instituciones simples, algunas previas al mapa, como puedan serlo las orientaciones vectoriales «hacia la derecha», «hacia la izquierda», «hacia arriba», «hacia abajo», «hacia delante» o «hacia atrás» (en el caso de las esferas armilares). Estas orientaciones elementales (que pueden estar institucionalizadas, pero que por sí mismas no constituyen un mapa), han de encadenarse entre sí para formar o conformar el mapa. Los mapas deben estar orientados precisamente según estas direcciones.
(3) La tercera característica del mapa es la de su imprescindible concatenación con otras instituciones: instrumentos de grabación, tejidos, senderos, caminos, rutas marítimas, señalizaciones en el campo, en la tierra, en el mar o en el cielo, y, por supuesto, en los ríos o en las posadas. En el mapa se cumple puntualmente el principio de que «andar es reandar»; al margen de este principio no habría mapas.
(4) Como cuarta característica institucional del mapa citaremos su racionalidad, que definiríamos principalmente en función de los itinerarios previstos por los sujetos que lo utilizan, así como en función de la incompatiblidad o de la coherencia entre ellos. El mapa pretende eliminar el azar de los itinerarios, los rumbos aleatorios. Por ello el mapa ha de ser verdadero (decisible) dentro de una franja de verdad variable. La verdad del mapa no reside tanto en su adecuación al terreno cuanto en el ajuste propio de las relaciones del terreno y de las secuencias operatorias del demiurgo.
La racionalización también implica los momentos generales de la racionalidad dialéctica: el momento de la posición o composición de los puntos del mapa y los del campo, y recíprocamente; el momento de la contraposición de los grafos del mapa, y las acciones en el campo; el momento de la recomposición controlada con las rectificaciones pertinentes.
(5) Como quinta característica señalamos la normatividad del mapa, que no se deriva estrictamente de su verdad, como correspondencia, sino que incluye la coherencia entre el seguimiento de las indicaciones del mapa en determinados tramos.
(6) La sexta característica institucional del mapa estriba en el valor de sus normas: la normatividad del mapa no puede ser aceptada ciegamente, sino que ha de estar corroborada en cada momento en función de las secuencias operatorias del demiurgo.
5. Desde la definición unívoca del mapa que hemos dibujado, se comprenderá que no todos los conónimos citados pueden ser considerados mapas en sentido unívoco. Pongamos algunos ejemplos.
Ejemplo 1. El célebre «mapa de Royce» (un mapa que «se representa a sí mismo», inaugurando un proceso ad infinitum), al que nos hemos referido en el artículo antes citado sobre el Ego trascendental (pág. 6), no satisface el concepto unívoco de mapa. Ante todo, porque el mapa de Royce no es un grafo o un dibujo (ni puede serlo) sino la descripción, en lenguaje de palabras, de un mapa imposible que se representase a sí mismo sobre el terreno. Imposibilidad implicada en la misma definición de Royce. La descripción verbal llamada «mapa de Royce» sólo es mapa en sentido analógico, es decir, como una modulación de la idea de mapa mediante el desarrollo límite de la relación aliorelativa como reflexiva, desarrollo que lleva al mapa a dejar de serlo (a la manera como el triángulo birrectángulo deja de ser un triángulo «dibujable»). El mapa de Royce es un mapa por analogía de atribución, por cuanto parte del concepto de mapa geográfico ordinario, pero no es «dibujable».
Ejemplo 2. Los «mapas neurológicos», de los que han hablado abundantemente neurólogos como Antonio Damasio o como Francis Crick, no son propiamente mapas. En efecto, la operación «cartografiar» que conduce al desarrollo de los mapas neurológicos se define por Crick (The Astonishing Hypothesis, págs. 172-173 de la edición española, Debate, Madrid 1994) como una información retiniana ofrecida («cartografiada») en el LGN (núcleo lateral geniculado) del tálamo en el área VI del córtex estriado (antigua área 17). «Se trata, desde luego, de un mapa de la mitad opuesta del campo visual, pero el mapa no es uniforme.» (Figura 45, reproducida arriba, §I:24.)
Ahora bien: la «información» que LGN ofrece al área VI no es una relación sino una conexión física, en la cual sólo cabe hablar de representación o mapa si la parte LGN del tálamo fuera un sujeto operatorio capaz de seleccionar los puntos que trataba de aplicar al área VI. Pero decir que LGN informa al área 4 de VI («cuyas neuronas escuchan lo que les dice LGN») es una grosera prosopopeya antropomórfica, porque esas partes del tálamo cerebral ni ven, ni miran, ni oyen, ni escuchan. Sin embargo, el mapa neurológico de Crick es un mapa dibujado en forma de mapa por Crick, y no por su tálamo o por su área VI. Tal es el mapa que figura en el libro que contiene la reproducción anterior. En cuanto mapa neurológico, el mapa de Crick es un mapa metafísico, en el cual las zonas del cerebro que interactúan se han hipostasiado como si fueran demiurgos de un mapa positivo.
Ejemplo 3. Cuando hablamos de «mapas ontoteológicos», como pueda serlo el mapa de Roberto Flud que antes hemos citado, en su libro Utriusque cosmi, los mapas tienen como dominio el dibujo o grafo. Pero el mapa de Flud carece de codominio, porque los triángulos, las personas divinas, que en él son aludidas, no son objetos corpóreos finitos susceptibles de ser representados.
Esta «anomalía» que advertimos en los mapas ontoteológicos nos permite aproximar la crítica a los mapas ontoteológicos a la crítica que los iconoclastas dirigieron contra los ídolos, considerándolos como «falsos íconos». Orígenes y Leoncio de Neápolis distinguieron, en efecto, entre ídolos e íconos, e impugnaron la iconoclastia de los judíos (Moisés, Exodo, 20,4), de los musulmanes o de los nestorianos, según los cuales Cristo, al tener dos naturalezas, una divina y otra humana, sólo podría representarse en cuanto hombre, pero no en cuanto Dios. Pero los propios teólogos suscitaban la cuestión filosófica de la razón por la cual Cristo era irrepresentable: ¿por ser incorpóreo o por ser infinito? (remitimos a nuestro trabajo «Los valores de lo sagrado: númenes, fetiches y santos», en Actas del congreso: Los valores en la ciencia y la cultura, León 2000, pág. 432).
Sin embargo, los argumentos contra la representación de lo infinito o de lo incorpóreo, suscitados por los iconoclastas, aplicados a los mapas, parecen basarse en un concepto de mapa según el cual los significantes (grafos, dibujos) debiera ser siempre idénticos o isomorfos a los significados (es decir, al campo del mapa). Pero este supuesto es gratuito. La muela dañada no puede representar al dolor de muelas, porque la muela (como significante) no contiene en su estructura ósea al dolor. El dolor se asocia a la muela por el sujeto que padece o por quien contempla a quien lo padece. Los grafos o dibujos corporales pueden representar al campo cuando el sujeto operatorio los inserta de algún modo en ese campo.
Ejemplo 5. El mapamundi sólo es mapa en sentido analógico, y no en sentido unívoco. El mapamundi (salvo para quien reduzca el «Mundo» a «Gea») no es un mapa, porque carece de campo sobre el cual fijar sus grafos. El mapamundi no es un mapa por la misma razón que el decaedro regular no es un poliedro.
Un mapa delimita su dominio dentro de un campo presupuesto: el mapa de la Tierra (del Globo) contiene necesariamente algo de mapa celeste, por ejemplo, de la banda celeste que aparece en el horizonte marino como zócalo de una cúpula gigante que se apoyase sobre la Tierra. Pero el Mundo, en su totalidad, carece de entorno, el Mundo tiene unicidad, y los «otros Mundos» (los de Demócrito o los de Vilenkin) o bien carecen de contacto con el nuestro, y entonces son sólo mundos imaginarios, o bien tienen contacto con el nuestro, y entonces no son «otros Mundos» sino regiones lejanas del nuestro.
De hecho, el primero que hizo un mapamundi (según testimonio de Laercio y de Suidas) no fue un geógrafo, sino un metafísico, Anaximandro de Mileto; lo que es tanto como decir que el mapamundi de Anaximandro era un mapa tan metafísico como su apeiron y su cosmos.
El Mundo del mapamundi sólo puede concebirse desde su concavidad, es decir, desde dentro de su bóveda. Al carecer el Mundo de entorno, el mapamundi no puede apoyarse en un campo envolvente, y por tanto no puede orientarse, o situarse, no ya «ubicarse», en el espacio absoluto. Desde este punto de vista podríamos dar cuenta de la contradicción que encierra (ya en el terreno de la etimología), la expresión mapamundi, si tenemos en cuenta que el término mapa significaba originariamente, en latín, pañuelo, por lo que «mapamundi» equivaldría al proyecto absurdo de «meter el Mundo cósmico en un pañuelo». El mapamundi elimina la posibilidad de asignar su dibujo (su grafo) al campo presupuesto.
§ 3
El mapa desde una
perspectiva gnoseológica
1. Los mapas son instituciones pragmáticas, cuya presencia se hace notar en muy diversas categorías, no sólo en las geográficas. Y esta es la razón por la cual podemos considerar al mapa como una figura gnoseológica (presente en diversas ciencias).
En todo caso, los mapas pueden constatarse en instituciones que no son propiamente científicas, como sería el caso del croquis del explorador, al que antes nos hemos referido. Según esto, un «mapa», como institución, no es por sí mismo una idea gnoseológica, aunque este mapa sea preciso, exacto, verdadero. El mapa nos remite antes a contextos tecnológicos que a contextos científicos.
Pero esto no excluye la posibilidad de que diversas ciencias categoriales tengan que incorporar mapas a sus construcciones, como es el caso de la Geografía, de la Cosmología, de la Anatomía o de la Neurología. Más aún, muchas ciencias categoriales necesitan enfrentarse con mapas que ya no pueden considerarse unívocamente tales, sino sólo analógicamente, y no por motivos extrínsecos (por ejemplo, didácticos, literarios o metafísicos) sino en virtud de una dialéctica interna, como es el caso de los que llamaremos mapas-límite. Tal es el caso del mapamundi de Anaximandro, ya mencionado, o el de los mapas reflexionantes, como el mapa que imaginó Royce, y cuyo grafo nadie puede dibujar.
2. Esto obliga a plantear la cuestión de las figuras o «cauces» a través de los cuales los mapas podrían entrar en un proceso de cierre categorial o, al menos, en un proceso de cierre tecnológico.
Y, puesto que, como hemos dicho, los mapas no son instituciones que se agotan en el recinto de un campo categorial (como pudiera serlo el de la Geografía), los cauces habrán de ser también comunes a diversas ciencias. Ello nos permite acudir a la teoría de los modos gnoseológicos, que distingue cuatro modos fundamentales: (1) el de los modelos (subdivididos en cuatro tipos: metros, paradigmas, prototipos y cánones), (2) el de las clasificaciones (también subdivididas en cuatro tipos: taxonomías, tipologías, desmembramientos y agrupamientos), (3) el de las definiciones y (4) el de las demostraciones (remitimos al volumen 1 de Teoría del cierre categorial, págs. 141-143).
Los mapas, según esto, podrían interpretarse gnoseológicamente o bien como definiciones, o bien como modelos, o como clasificaciones o como demostraciones.
En su obra ya citada, Utriusque cosmi (1617), Roberto Flud nos ofrece un mapamundi ontoteológico (que hemos reproducido antes) que es presentado como Demostratio; es decir, como si el mapa ofrecido gráficamente constituyese la demostración de las ideas ontoteológicas presupuestas. Teniendo en cuenta que el mapa de Flud es un mapa metafísico –por tanto, no es un mapa en sentido unívoco, sino analógico–, tendríamos que interpretar el término «demostratio», antes como una figura pedagógica o heurística que como una figura gnoseológica. Como si con su demostratio, el mapa ontoteológico de Flud no hubiera pretendido probar sus ideas, sino simplemente ilustrarlas, hacerlas accesibles a los lectores, por analogía a como se ilustran en los mapas geográficos las zonas invisibles de la Tierra.
Tampoco es fácil reducir los mapas al modo de las definiciones, porque un mapa, sin duda, define o delimita un dominio dado en un campo, pero no se agota en esa delimitación.
Nos inclinamos, en conclusión, a interpretar los mapas, cuando puedan ser considerados como contenidos de un cierre categorial, como modelos (que suponemos se corresponden a functores predicativos, que forman predicados o relaciones a partir de términos) y como clasificaciones (correspondientes a los functores determinativos, que forman términos a partir de relaciones).
3. Ahora bien, de la consideración de la mayoría de los mapas como procedimientos de clasificación no cabe deducir que toda clasificación científica tenga, por sí misma, la estructura unívoca del mapa (aún cuando pueda mantener determinadas analogías con él). Una clasificación científica no tiene por qué asumir la estructura unívoca del mapa como institución pragmática, en la cual su grafo o dibujo involucra al sujeto operatorio que lo utiliza como instrumento para organizar itinerarios en el campo correspondiente (aunque estos itinerarios consistan en el giro del telescopio que inspira un mapa celeste). Una clasificación científica puede mantenerse al margen del eje pragmático, como representación pura o especulativa, α operatoria, es decir, entre objetos, sin involucrar las operaciones del sujeto β operatorio.
Consideremos el caso de la clasificación de los elementos químicos, dando por supuesto, desde luego, que el llamado «sistema periódico» es una clasificación pero no un mapa (sin perjuicio de notables analogías con los mapas, en sentido unívoco). Nadie pondrá en duda la afirmación de que la clasificación de los elementos químicos, contenida en el sistema periódico, es una clasificación científica. Y, más aún, la clasificación a través de la cual la Química de los elementos se constituyó como una ciencia rigurosa y cerrada, siquiera fuera en estado embrionario.
La sospecha de que los elementos químicos que –una vez rotos cada uno de los cuatro elementos de Empédocles/Aristóteles–, venían acumulándose tras los descubrimientos del siglo XVIII y primera mitad del XIX, pueden ordenarse no ya por la simple sucesión de sus fechas de descubrimiento, o por la sucesión alfabética de sus nombres, sino por un orden que tuviese que ver algo intrínseco a los propios elementos, tomó cuerpo en su forma mas sencilla en la sugerencia de J. H. Gladstone, en 1853, según la cual los elementos podrían ordenarse según la sucesión lineal constituida por los números correspondientes a sus pesos atómicos. Esta sucesión lineal era representable en una única línea trazada en un plano, tal como el plano de una página desplegada. Sin duda, la ordenación lograda por este criterio lineal, representada además por una línea del plano gráfico, tenía bastante de mapa cuyo grafo se mantuviese en E1, o, por lo menos, podría ser utilizada como tal por un sujeto operatorio.
Sin embargo, esta ordenación lineal de los elementos (cuyo principio ya no se perdería, puesto que la ordenación líneal de los elementos se mantendrá posteriormente, cuando la línea se «curve» en los sucesivos tramos o periodos de la tabla periódica) no era capaz de representar el «hecho químico» decisivo, a efectos estructurales, del proceso, a saber, la repetición de ciertos caracteres esenciales de naturaleza química. Un hecho que no tenía paralelos rigurosos fáciles de encontrar, salvo en la sucesión lineal de las alturas de la escala musical, que mantenía su curso ascendente o descendente. Como es sabido este paralelismo entre la ordenación de los elementos químicos y la ordenación de las alturas de los sonidos fue advertido por J. Newlands, que ya en 1864 habló, no ya sólo de repetición periódica de ciertas propiedades, sino de repetición por octavas (las «octavas» de Newlands); pero esta observación no pasó del plano fenomenológico.
Fue Mendeleiev quien en 1869 logró determinar dos criterios (aún sin poder todavía justificar estos criterios en la estructura de los elementos químicos), a saber, en primer lugar el criterio de los periodos, derivados de su ordenación según los números atómicos (que se designarían después por la letra Z), que (una vez consolidada la teoría del átomo de Rutherford) se harían corresponder con el número de electrones. Un número que iba aumentando conforme aumentaba el peso atómico, lo que permitía la clasificación de los elementos de la serie continua en periodos de ocho elementos (al menos para las tres primeras filas de la tabla). En segundo lugar, el criterio de los grupos, que clasificaba a los elementos de cada columna de la tabla según determinadas características que atravesaban, en vertical, a los periodos.
La composición de estos dos criterios permitió ya levantar una tabla de clasificación, cuyo paralelo con la música desbordaba ampliamente el alcance de los periodos advertidos por Newlands. Ahora teníamos que comparar la ordenación de los elementos, no ya a la serie lineal, melódica, de sonidos, con sus repetidos periodos, procedentes de un mismo instrumento, sino con las marchas armónicas de una sinfonía en la que interviniesen varios instrumentos.
Las filas de la Tabla periódica se corresponderán, de este modo, con la línea melódica horizontal de la partitura, y las columnas de la tabla se corresponderán con las líneas verticales de esa partitura. Sólo después de Rutheford y de Bohr pudo ofrecerse una razón para establecer la correspondencia entre el desarrollo lineal de Z (correspondiente como número atómico, al número creciente de los electrones de los átomos en función del incremento de los pesos atómicos, designados por A, y que, obviamente, no dependen sólo de los electrones, sino del número de neutrones N que el incremento de electrones del átomo implicaba, según la fórmula A=Z+N). La línea representativa de la serie de electrones «iría plegándose» en sucesivas capas (K, L, M, N, O, P, Q) hasta que la «capa cortical» o externa (en cada momento) llegase a los ocho electrones, lo que se cumplía rigurosamente en los tres primeros periodos: el periodo 1 (1 H, 2He), el periodo 2 (3 Li, 4 Be, 5 B, 6 C, 7 N, 8 O, 9 F, 10 N) y el periodo 3 (desde el 11 Na hasta el 1 A).
Por supuesto, ni la tabla periódica ni la partitura sinfónica, aunque sean clasificaciones, tienen por qué ser mapas, en el sentido unívoco definido. Pero precisamente porque su alcance α-operatorio permite abstraer los componentes β-operatorios propios de todo curso pragmático. Por ello no se excluye la posibilidad de que la partitura sinfónica sea, en sentido analógico (cambiando el espacio por el tiempo), utilizada por el director de la orquesta o por los músicos como un «mapa» en el que situar (y no sólo ubicar) el sonido puntual de una flauta o un acorde determinado, en el conjunto de la sinfonía.
4. En cualquier caso, el alcance científico de los mapas (y de los mapas en ejercicio pragmático, es decir, de los mapas utilizados por geógrafos, viajeros o navegantes, por tanto, de los mapas considerados juntamente con las intervenciones efectivas del sujeto operatorio en su campo) parece fuera de toda duda. Por nuestra parte, a raíz de Quinto Centenario del Descubrimiento de América, defendimos el alcance que la concepción esférica de la Tierra (procedente de Eratóstenes, de Posidonio, de Tolomeo) había que atribuir a la formación misma del concepto geográfico de «América» y, por tanto, de su descubrimiento. Lo que contribuyó a manifestar la imposibilidad de los proyectos que en aquéllos años renacieron con fuerza, por parte de algunos indigenistas americanos, de «descubrir o redescubrir Europa» viajando en canoas, como si el continente europeo o el americano fuesen «visibles» a tiro de piedra, o tangibles, en un tiempo en el que todavía no existían los satélites espaciales, capaces de distanciarse de la Tierra a una escala tal que permita fotografiarla a escala continental.
Pero, sobre todo, subrayábamos cómo la concepción de la esfericidad de la Tierra y las medidas de Eratóstenes, Posidonio o Tolomeo, o de cualquier otro, hasta Elcano, no podrían considerarse científicas, sino meras especulaciones hipotéticas (por ingeniosas que fueran) de astrónomos griegos o continuadores. Hipótesis especulativas que únicamente podrían comenzar a transformarse en tesis científicas precisamente a partir de la primera circunvalación de la Tierra, en 1521, subsiguiente al descubrimiento de América, en 1492, por la nao Victoria (remitimos a nuestro artículo «La Teoría de la Esfera y el Descubrimiento de América», El Basilisco, 2ª época, nº 1, páginas 3-32).
El hecho, constituido por la serie de operaciones implicadas en la circunvalación del Victoria, considerado desde una teoría de la ciencia materialista (en la cual las «morfologías del Mundo» no son meramente re-presentadas por las ciencias –por ejemplo, por los grafos de mapas, o, si se prefiere, por los «grafos mapológicos»– sino que son partes de la ciencia misma), postulaba en realidad la necesidad de considerar el descubrimiento de América no ya tanto como un «hecho» meramente político o económico o religioso, sino sobre todo como un acontecimiento científico, aunque los historiadores de la ciencia, que utilizan teorías gnoseológicas idealistas, no fueran capaces de incorporar este hecho a sus esquemas.
La naturaleza científica del acontecimiento del hecho de la circunvalación puede cifrarse en la circunstancia mediante la cual una hipótesis astronómica (la esfericidad de la Tierra, que había servido ya a Colón para llevar a cabo su descubrimiento) que por sí misma no demostraba la esfericidad, puesto que la presuponía (dado que partía de ella y, a lo sumo, la hacía más «probable»), quedaba transformada en tesis. Nos remitimos en este punto a los importantes y pertinentes desarrollos de esta cuestión ofrecidos por Lino Camprubí Bueno en su trabajo «Viaje alrededor del Imperio: rutas oceánicas, la esfera y los orígenes atlánticos de la revolución científica» (El Catoblepas, nº 95:1, enero 2010).
§ 4
Los «mapas analógicos»
del materialismo filosófico
1. Quien quiera que se haya asomado a las exposiciones del sistema denominado «materialismo filosófico» habrá podido advertir la presencia de figuras semejantes o análogas a las de los grafos de los mapas tomados en sentido unívoco.
A veces son «grafos algebraicos» o «mapas anicónicos» (que hemos incluido como epígrafe § I, 3.30 entre los mapas), como pueda serlo el grafo de la ontología general del materialismo constituido por la secuencia séxtuple de letras:
< M, Mi, (M1, M2, M3), E >
No vamos a analizar aquí la estructura de este mapa ontológico anicónico y las relaciones o conexiones con los otros mapas considerados del materialismo filosófico. Tan sólo diremos que el mapa ontológico algebraico que contiene las «ideas claves» lisológicas del materialismo (M, M1, M2, M3), está «orientado» desde la perspectiva de su núcleo [Mi (M1, M2, M3)], que aparece flanqueado por M (a la izquierda) y por E (a la derecha). Mi es, de algún modo, el campo gnoseológico positivo propio del materialismo filosófico, que corresponde a la idea de Universo antrópico (Mi), cuyos Géneros de materialidad (M1, M2, M3) no cabe identificar con ninguno de los ejes del espacio antropológico, pero no porque se mantengan al margen de ellos, sino porque al atravesarlos se determinan morfológicamente a través de ellos (por ejemplo, M1 no se agota en los entes corpóreos no vivientes asignables al eje radial, porque también comprende a los entes corpóreos vivientes orgánicos, e incluso a los entes incorpóreos tales como ondas electromagnéticas o campos de fuerza, asignables al mismo eje radial; M2 tampoco «se agota» en el eje circular, sino que penetra en el eje angular; M3 atraviesa los tres ejes del espacio antropológico, en tanto compromete tanto las leyes cristalográficas, «radiales», como las leyes de dominación, «angulares», o las legalidades políticas, «circulares»). La secuencia algebraica ofrece el núcleo Mi como «envuelto» por M en el regressus ontológico (sin progressus morfológico posible), y orientado en el regressus gnoseológico con progresos ejercitados permanentemente por E. Por lo demás, el núcleo algebraico del mapa ontológico adolece de las distorsiones propias de la perspectiva que equipara, por ejemplo, en el grafo, la amplitud algebraica de M2 a la de M1; distorsiones de origen análogo a las que hemos advertido en los homúnculos neurológicos (tanto en el homúnculo somatoestético como en el homúnculo motor de W. G. Penfield).
Por supuesto, los mapas analógicos considerados en este párrafo no se entienden como mapas en sentido unívoco, sino análogo. Y, sin embargo, tampoco se trata de figuras utilizadas con intención meramente didáctica o heurística, puesto que tienen un alcance doctrinal, en cuanto recursos a veces insustituibles en el momento de delimitar ideas o conceptos ontológicos.
2. Tal ocurre, ante todo, con el «mapa» mediante el cual tiene lugar la exposición de la doctrina del «espacio antropológico» (en cuanto idea contradistinta a la de «material antropológico»), que hemos reproducido al principio de este rasguño.

Mapa del espacio antropológico (El Basilisco, nº 5, 1978, página 58.)
Conviene subrayar que ya la utilización de la idea de espacio (en la expresión «espacio antropológico») en lugar de «Hombre» envuelve una concepción ontológica pluralista (no monista, como cuando se define la «Antropología» por el «Hombre»), porque «espacio» está entendido allí (y así se hacía constar explícitamente) como una unidad que se despliega en una symploké de direcciones diversas, «engranadas», como una pluralidad de vectores (arriba/abajo, izquierda/derecha, delante/atrás) vinculados a contenidos físicos que mantienen independencia (o discontinuidad) los unos de los otros, y son susceptibles de ensamblarse (de componerse, de neutralizarse) en totalidades más amplias. Dicho de otro modo: «espacio antropológico» dice antes «pluralidad del material antropológico», que unidad desplegada de una supuesta esencia unitaria previamente dada (como lo era el «Hombre», directamente creado por Dios, en la tradición filosófica escolástica).
El alcance gnoseológico de este mapa del espacio antropológico puede medirse por el hecho de que las denominaciones de los componentes fundamentales de la idea del espacio antropológico, a saber: la propia idea de espacio, a la que nos hemos referido, y las ideas de «eje circular», de «eje radial» y de «eje angular», están tomadas precisamente del diagrama o grafo de la figura. Es decir, no reciben nombres de ideas procedentes de fuentes ajenas al mapa, como ocurriría si en lugar de hablar de «espacio» hablásemos de «sistema»; o de si en lugar de hablar de «eje circular» hablásemos, por ejemplo, de «relaciones o conexiones interpersonales», en general; o de si en lugar de hablar de «eje radial» hablásemos de «Mundo entorno inanimado de los hombres»; o de si en lugar de hablar de «eje angular», hubiéramos hablado del «Mundo entorno viviente de los hombres».
Ahora bien: si no recurríamos a estas denominaciones, o a otras similares, era por motivos críticos, es decir, por la necesidad de desvincular la idea del «espacio antropológico» respecto de los sistemas metafísicos tradicionales, a los cuales se enfrenta la doctrina del espacio antropológico. Por ejemplo, el sistema tradicional de las tres ideas de la ontología metafísica tradicional (Santo Tomás, F. Bacon, Ch. Wolff, Kant).
En el momento en el que hubiéramos hablado de «Hombre», o de «Mundo» o de «Dios», nos estaríamos situando en las coordenadas metafísicas implicadas por dichos términos; coordenadas, sin embargo, de las cuales partimos necesariamente, puesto que no es posible partir del «conjunto cero de premisas».
Esta es la razón por la cual tuvimos que considerar, en su momento, miopes, a ciertas críticas ingenuas de quienes (como Quintín Racionero) interpretaron las referencias a Wolff, que constaban ya en Ensayos materialistas (Madrid 1972), como si la ontología propuesta en tales Ensayos fuera wolfiana o prekantiana, y como si Kant mismo no hubiera tenido presente a Wolff en la exposición de su «sistema de las tres ideas» de la razón pura. O si, por el hecho de seguir alguien denominando a las ideas de este sistema como «idea antropológica», «idea cosmológica» o «idea teológica», asumiese inmediatamente la perspectiva metafísica.
Pues no se trataba simplemente de cambiar el «lenguaje heredado», sino de triturar las ideas asociadas a tal lenguaje. No se trataba, en nuestro caso, de «sustituir» el término Sistema por Espacio, el término Hombre por Eje circular, el término Mundo por Eje radial y el término Dios por Eje angular, puesto que lo que se estaba cambiando era la propia perspectiva ontológica desde la cual se configuraban tales ideas. Teniendo en cuenta –y esto es esencial– que las nuevas denominaciones no se consideraban procedentes de una «revelación» inaudita (ofrecida desde «el conjunto cero de premisas»), sino de la trituración de ideas heredadas que, en cualquier caso, debían mantener profundas conexiones con los materiales involucrados con tales ideas heredadas.
Sin duda alguna los contenidos incorporados al eje circular debían tener mucho que ver con los contenidos interpersonales; los contenidos del eje radial habían de intersectar en muchos puntos con los que tradicionalmente formaban parte del Mundo físico, y los contenidos del eje radial con los contenidos de la teología o de la religión (pero no con la idea de Dios de la ontotelología, o con la idea tradicional de religión definida en función de «las relaciones del hombre con Dios»).
El espacio al que se aludía en la expresión «espacio antropológico» no era tampoco el espacio abstracto geométrico, o el espacio absoluto de Newton, o el espacio-tiempo de Minkowski, sino un espacio empírico tridimensional en el que confluían hombres, animales y númenes. Por supuesto, personas humanas, pero «recortando» de ellas la espiritualidad que le reconocen, por ejemplo, las tradiciones escolásticas o el dualismo cartesiano. Las personas humanas eran reconocidas en el eje circular antes como individuos animales que, a partir de un cierto estadio histórico de su evolución, entraban en contactos grupales o culturales, que como organismos a los que un creador les hubiera insuflado en su momento el espíritu.
3. Habría que tener en cuenta, por tanto, que el sistema de las tres ideas metafísicas (Hombre, Mundo, Dios) no era el resultado de una acumulación de ideas independientes, y menos aún el resultado de las «afinidades lógicas» entre supuestos silogismos categóricos, hipotéticos y disyuntivos, como pretendió Kant en ocurrencia idealista (cuanto a la génesis de las ideas respectivas) tan ingeniosa como enteramente gratuita.
Habría que dar por supuesto que el Mundo, en la metafísica tradicional, no era una idea independiente de Dios, puesto que la «totalización de las cosas visibles y sensibles» en la unidad del Mundo, implicaba (una vez retirada la idea del cosmos de Anaximandro o de Aristóteles) la idea de la creación ex nihilo del mundo por Dios, como ser supremo. Asimismo, la «idea moderna» de Hombre, como idea capaz de enfrentarse al mundo en su totalidad (tal como la expusieron, por ejemplo, Max Scheler o Arnold Gehlen), estaba envuelta en los dogmas cristianos de la unidad hipostática entre Dios y el Hombre a través de Cristo, como Segunda Persona de la Trinidad. Por ello, si al hablar del Hombre queríamos desentendernos de estas implicaciones ontoteológicas, se hacía prácticamente imprescindible, teniendo como fondo el material antropológico (empírico, histórico, &c.), hablar de un eje circular, de un eje radial y de un eje angular, aludiendo a la nueva perspectiva materialista, no monista.
Por ello resultaba imprescindible, por ejemplo, desvincular el Mundo (involucrado en el eje radial) respecto de Dios, y, por tanto, dejar de entender al Mundo como una realidad primera o absoluta surgida de la nada en virtud de un acto de creación de un Dios desconocido. El Mundo inorgánico o cósmico, involucrado en el eje radial, no sería por tanto el mundo anterior al hombre y a los animales, sino el Mundo antrópico (Mi), si bien no en el sentido del idealismo («el Mundo como representación de la realidad en los hombres o en los animales») sino en el sentido de que el Mundo (en cuanto totalidad de configuraciones tales como constelaciones estelares, árboles, fieras, &c.) no era la realidad absoluta aludida por el materialismo monista (M), sino una realidad Mi configurada a escala antrópica, en la que tanto las morfologías humanas como las planetarias, se suponen codeterminadas.
4. Y, sin embargo, el Mundo cósmico (inorgánico) implicado en el «eje radial» mantenía muchas cosas en común con el mundo cósmico implicado en la concepción tradicional, tanto en la del materialismo monista como en la del espiritualismo de la ontoteología.
De algún modo cabría decir que se trataba del mismo «mundo», pero considerado desde perspectivas diversas. Una diversidad que se manifiesta esencialmente mediante la distinción entre el Mundo considerado desde una perspectiva convexa y el Mundo considerado desde una perspectiva cóncava. Es decir, entre el Mundo percibido como si estuviéramos en una cueva (distinción que, por cierto, es utilizada, a su escala, por los propios autores de los mapas o atlas astronómicos).
Una distinción que se aprecia claramente en las representaciones de las relaciones entre Dios y el Mundo de la tradición medieval y moderna, y las relaciones entre el Hombre y el Mundo en el espacio antropológico. Aquí se advierte claramente que el cambio de perspectiva no se reduce a «sustituir» a Dios por el Hombre; ni siquiera es suficiente referirse al cambio de un Dios acósmico, como pudiera serlo el Acto Puro de Aristóteles (que no sólo no ha creado el Mundo, pero que ni siquiera lo conoce), por un Dios cósmico orientado hacia el Mundo, tras la «inversión teológica» (remitimos aquí a nuestro Ensayo sobre las categorías de la economía política, Barcelona 1972, pág. 133). No se trata, en efecto, de sustituir por otra la orientación tradicional del Dios cristiano hacia el Mundo (aunque el cambio de orientación, contenido en la «inversión teológica», pueda seguir reconociéndose como un cambio significativo en la historia fenomenológica de las ideas). Se trata de sustituir la perspectiva misma desde la cual se nos conforma la idea del Mundo.
5. Comparemos, a este efecto (aunque en esbozo), las representaciones del Pantocrátor (como formas de entender las relaciones positivas entre Dios omnipotente, en la figura de Cristo, y el Mundo) a lo largo de la iconografía escultórica o pictórica del arte medieval y moderno. El Pantocrátor es la imagen de Dios omnipotente, en la figura de Cristo, que se representa a la Tierra, incluso al Mundo que gira en torno a ella, antes de Copérnico o Galileo, como si estuviese mirándolo desde fuera de él, en su convexidad, como mira a una esfera (la «bola del mundo») que Él hubiera creado.

Pantocrátor del pórtico de San Juan Bautista, Moarves de Ojeda, Palencia.
Durante los siglos medievales el Pantocrátor sostiene entre sus manos un Libro (los Evangelios, si tenemos en cuenta las figuras tetramorfas que suelen rodear a la representación). La presencia de este Libro pudiera interpretarse en el sentido de que este género de Pantocrátor se dirige al Mundo desde una perspectiva «convexa», exterior, que sin embargo presupone que en ese Mundo viven personas humanas capaces de leer, puesto que el Pantocrátor les ofrece un libro.

Pantocrátor de la iglesia de Bordón, Teruel.
Ahora bien, a partir del siglo XV, parece como si el libro del Pantocrátor fuese desapareciendo, y que Dios comenzase a tomar en sus manos a la misma esfera cósmica, a la bola del Mundo. Parece evidente que la influencia del Pantocrátor sobre el Mundo no se limitará, ahora, a revelar un libro a las personas humanas que en el Mundo viven, sino a ejercer en la esfera cualquier género de influencia, o de dominación. La omnipotencia del Pantocrátor, aunque mantiene la perspectiva convexa sobre el Mundo, afecta ya a todos sus contenidos, a las personas, a los animales y a las cosas. Especialmente a las «cosas políticas». Este punto de vista permanecerá en los siglos posteriores, en los cuales el Pantocrátor comienza a verse como Cristo-Rey.

Cristo Rey pantocrátor: Jesus Christus Rex Regum.
No entraremos aquí en la cuestión de las causas que pudieron determinar el cambio, en las manos de Cristo, del libro por la esfera. ¿Se trataba del cambio de una dominación apostólica y pacífica, mediante un libro, hacia una dominación política y violenta si fuera preciso? Y, ¿qué conexiones pudieron tener estos cambios con la entrada en América y con su conquista? La pregunta parece pertinente en la medida en la que el descubrimiento tuvo implicaciones muy profundas en la visión del Mundo en cuanto esfera finita (incluso cuando la esfera comprendía –como en el caso de la representación de Fernando Gallego en su tabla Cristo bendiciendo, en el Museo del Prado, realizada por los años del Descubrimiento– no solamente la esfera terrestre, sino también, en la tradición aristotélico tolemaica, las esferas cristalinas que la envuelven, comprendida la esfera de las estrellas fijas).

Fernando Gallego (c1440-1507), Cristo bendiciendo (fragmento)
(Museo del Prado, Madrid).
Supuesta esta perspectiva, que la ontoteología tradicional puede ofrecer del Mundo cósmico, la visión del Mundo cósmico que nos ofrece el eje radial del espacio antropológico podría caracterizarse no ya por la sustitución de Dios por el Hombre, sino por la sustitución de la perspectiva convexa por la perspectiva cóncava (o, si se prefiere, como un cambio de la visión del Mundo desde una perspectiva semántica –en la que se han segregado los sujetos operatorios– por una perspectiva pragmática, en la que es imprescindible la referencia a los sujetos operatorios).
Desde la idea de un espacio antropológico el Mundo no es representable como una esfera que pueda ser vista «desde fuera», desde su superficie convexa. Esta es la visión que se atribuye al Dios creador, o a la de un hombre identificado con ese Dios, que no será el Dios eterno de Aristóteles, pero sí el «Dios haciéndose a través del Mundo y del Hombre» de Sabelio o de Hegel.
Desde el espacio antropológico, el eje radial nos lleva a una representación del mundo cósmico como si fuera una realidad contemplada desde dentro de ese Mundo, de un mundo que ni siquiera ha de entenderse como un «envolvente» de esos hombres que proceden de la evolución darwiniana interna del Mundo cósmico, sino como una conformación de una realidad M de la cual han de «emanar» tanto las formas del Mundo cósmico como las formas del Mundo humano, y, en especial, las llamadas «morfologías culturales».
Concluimos: el «mapa» involucrado en la idea de espacio antropológico no pretende ofrecer tanto una representación directa de la realidad antropológica, o del material antropológico, cuanto una representación indirectamente ejercitada a través de la crítica (con pretensiones de crítica trituradora) de los «mapamundi convexos» de la tradición ontoteológica heredada, y de su visión del mundo físico desde una perspectiva convexa (la del Pantocrátor), considerada como absurda, desde el momento en que el Mundo carece de entorno, y, por tanto, desde el momento que a los hombres les es imposible «salir fuera del Mundo», aunque sea para contemplarlo desde su misma supuesta convexidad.
6. El espacio gnoseológico es una clasificación, sin duda, pero susceptible de ser presentada mediante un grafo o dibujo que la asemejan, analógicamente, a un mapa. A un mapa E3, con tres ejes ortogonales, un eje sintáctico, un eje semántico y un eje pragmático, divididos cada uno en tres figuras (remitimos al volumen 1 de Teoría del Cierre Categorial, Oviedo 1992, página 116).
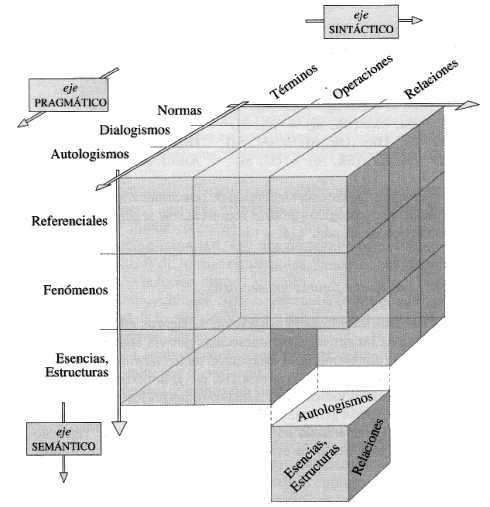
Gustavo Bueno, Teoría del Cierre Categorial, Oviedo 1992, pág. 116.
Este espacio gnoseológico puede ponerse en correspondencia con el espacio político (que representamos, en las obras citadas, como un eneaedro). El espacio gnoseológico tiene tanta afinidad con el espacio político por lo menos como pueda tenerla con el espacio cibernético o con el espacio teológico (remitimos a Panfleto contra la democracia, Madrid 2004, pág. 124, y también 108 y 110).

Gustavo Bueno, Panfleto contra la democracia, Madrid 2004, pág. 124.
7. Obviamente, las correspondencias entre el espacio antropológico y el espacio político, no tienen por qué ser biunívocas. Pongamos por caso, no tienen por qué ser correspondencias entre el eje radial del espacio antropológico y el eje basal del espacio político; o bien, entre el eje angular del espacio antropológico y el eje cortical del espacio político.
Las correspondencias, sin embargo, se mantienen por vías más complicadas, por ejemplo, las correspondencias obtenidas tras la «suma» de la capa conjuntiva y de la capa basal, o bien, tras la «suma» de la capa conjuntiva y la cortical, o tras la «suma» de la capa basal y la cortical (como se sugiere en el Panfleto contra la democracia, págs. 127 y 128).
El análisis de las correspondencias entre el espacio antropológico y el espacio político aparece ya como propuesta sistemática en el Primer ensayo de las categorías de las ciencias políticas (Logroño 1991, a partir de la página 274 y, sobre todo, desde la página 307 y ss., por ejemplo en las páginas 324 y 346).

Gustavo Bueno, Primer ensayo de las categorías de las ciencias políticas, Logroño 1991, página 324
También en este libro se planteó el análisis de las correspondencias entre el espacio político y el espacio gnoseológico (cuestiones sintácticas, pág. 52; cuestiones semánticas, pág. 76; cuestiones pragmáticas, pág. 103). En la tabla-mapa de la página 324 se cruzan criterios correspondientes a los ejes del espacio antropológico, para definir las capas del espacio político (circular/conjuntiva, radial/basal, angular/cortical) y criterios tomados del espacio gnoseológico, para diferenciar sus ramas (términos/poder determinativo; relaciones/poder estructurativo; operaciones/poder ejecutivo).
Dejamos para otra ocasión análisis más pormenorizados de estas cuestiones.
Sin embargo, nos arriesgamos a concluir, que la Idea analógica de mapa es una idea lisológica esencialmente confusa y oscura, sin por ello dejar de ser una idea objetiva inevitable, que se realimenta dialécticamente y continuamente del concepto tecnológico de mapa geográfico local o regional definible como reproducción o mímesis esquemática (gráfica o pictórica) de un terreno delimitado según criterios extrínsecos al propio grafo del mapa. De este modo tampoco cabe concluir que el mapa geográfico estricto (unívoco) constituya un concepto estable, científico o cerrado, de mapa, puesto que, por naturaleza, el mapa tecnológico no tiene unos límites fijados «desde dentro», y sus componentes son siempre susceptibles de desarrollos tales que sean capaces de desbordar los límites presupuestos, de manera tal que será preciso reconocer, en los propios mapas técnicos, los gérmenes de su transformación dialéctica interna desde su estado de concepto positivo de mapa hasta una idea de mapa derivada de ellos, pero capaz de desarticular por completo el mapa como concepto positivo, al que habrá que volver de nuevo, si no periódicamente, sí al menos cíclicamente. Estos ciclos constituyen un fundamento firme para asegurar la institucionalización indefinida de la idea de mapa.